【理論】令和5年(上期) 問5|直流電源を加えた抵抗の直並列回路における消費電力の計算問題
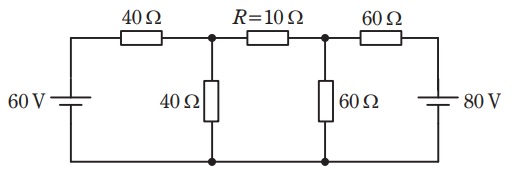
図の直流回路において,抵抗 \( R = 10 \) \(\mathrm{\Omega}\) で消費される電力の値 \(\mathrm{[W]}\) として,最も近いものを次の \( (1) \) ~ \( (5) \) のうちから一つ選べ。
合格への方程式
重ね合わせの理
重ね合わせの理とは、複数の電源を持つ線形回路において、各電源が単独で作る効果の和として回路全体の応答を表すことができるという原理です。
- 着目する電源以外の電源を無効化する
- 電圧源→短絡(0V)
- 電流源→開放(0A)
- 各電源ごとに回路応答(電流・電圧)を計算する
- 全ての応答を足し合わせて、最終的な応答を求める
- 重ね合わせの理は線形回路にのみ適用可能(非線形素子を含む回路には使用できない)
- 計算の手間を減らし、複雑な回路を解析しやすくする強力なツール
- 電源が多い場合でも各電源を個別に考えることで解析が容易になる
例題:重ね合わせの理の適用
複数の電源がある回路で、ある抵抗に流れる電流を求める場合:
- 電源1だけを有効にして電流I₁を計算
- 電源2だけを有効にして電流I₂を計算
- 最終的な電流 I = I₁ + I₂
電流の向きに注意して、同じ向きなら加算、逆向きなら減算します。
合成抵抗
複数の抵抗器が接続された回路では、それらを一つの等価な抵抗に置き換えることができます。接続方法によって計算式が異なります。
抵抗 \(R_1\) と \(R_2\) が直列に接続されている場合、合成抵抗 \(R\) は次式で表されます:
\[ \begin{aligned} R &= R_1 + R_2 \\[10pt] \end{aligned} \]
一般的に、n個の抵抗が直列の場合:
\[ \begin{aligned} R &= R_1 + R_2 + \cdots + R_n \\[10pt] \end{aligned} \]
抵抗 \(R_1\) と \(R_2\) が並列に接続されている場合、合成抵抗 \(R\) は次式で表されます:
\[ \begin{aligned} \frac{1}{R} &= \frac{1}{R_1} + \frac{1}{R_2} \\[10pt] \end{aligned} \]
整理すると:
\[ \begin{aligned} R &= \frac{R_1 R_2}{R_1 + R_2} \\[10pt] \end{aligned} \]
一般的に、n個の抵抗が並列の場合:
\[ \begin{aligned} \frac{1}{R} &= \frac{1}{R_1} + \frac{1}{R_2} + \cdots + \frac{1}{R_n} \\[10pt] \end{aligned} \]
例題:合成抵抗の計算
抵抗 \(R_1 = 100\Omega\) と \(R_2 = 200\Omega\) がある場合:
直列接続: \(R = R_1 + R_2 = 100 + 200 = 300\Omega\)
並列接続: \(R = \frac{R_1 R_2}{R_1 + R_2} = \frac{100 \times 200}{100 + 200} = \frac{20000}{300} \approx 66.7\Omega\)
- 直列接続:電流の通り道が長くなり、抵抗値が増加
- 並列接続:電流の通り道が増えるため、全体の抵抗値は減少
- 2つの同じ抵抗 \(R\) を並列にすると、合成抵抗は \(\frac{R}{2}\) になる
分圧・分流の法則
分圧の法則と分流の法則は、回路解析を簡略化するための基本原理です。これらを理解することで、複雑な計算を省略できる場合があります。
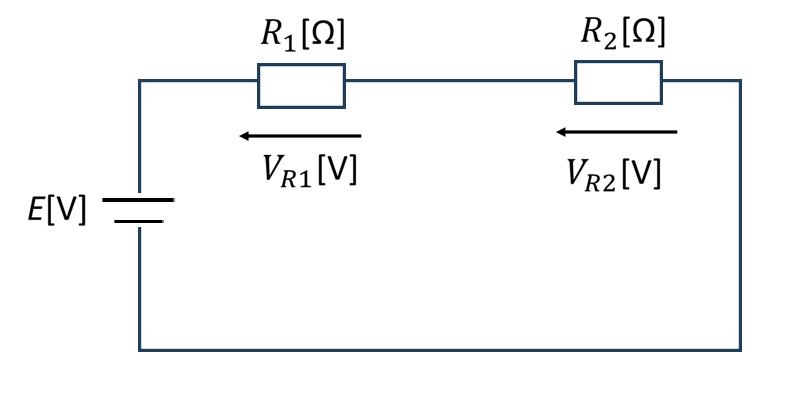
図2:分圧の法則
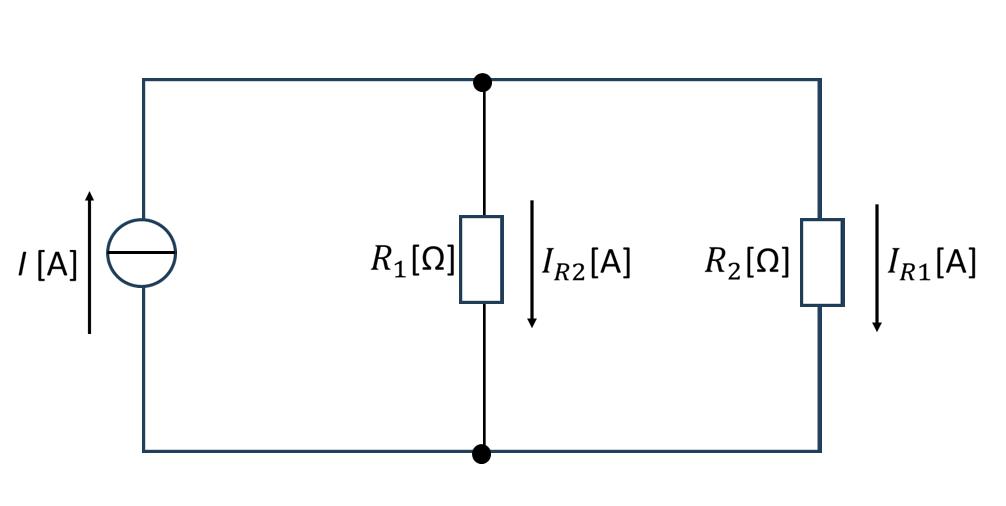
図3:分流の法則
直列接続された抵抗に電圧をかけると、各抵抗にかかる電圧は抵抗値に比例して分配されます。
図2のような直列回路において、各抵抗にかかる電圧は次式で表されます:
\[ \begin{aligned} V_{R1} &= \frac{R_1}{R_1 + R_2}E \\[10pt] V_{R2} &= \frac{R_2}{R_1 + R_2}E \\[10pt] \end{aligned} \]
ここで、\(E\) は電源電圧、\(V_{R1}\) と \(V_{R2}\) はそれぞれの抵抗にかかる電圧です。
並列接続された抵抗に電流を流すと、各抵抗に流れる電流は抵抗値に反比例して分配されます。
図3のような並列回路において、各抵抗に流れる電流は次式で表されます:
\[ \begin{aligned} I_{R1} &= \frac{R_2}{R_1 + R_2}I \\[10pt] I_{R2} &= \frac{R_1}{R_1 + R_2}I \\[10pt] \end{aligned} \]
ここで、\(I\) は全体の電流、\(I_{R1}\) と \(I_{R2}\) はそれぞれの抵抗に流れる電流です。
注意点: 分流の法則では、分子の抵抗が分圧の法則と逆になります(\(R_1\) と \(R_2\) が入れ替わる)。
例題:分圧・分流の法則の適用
分圧の例: 100Ωと200Ωの抵抗が直列接続され、全体に12Vの電圧がかかる場合
\[ \begin{aligned} V_{R1} &= 12 \times \frac{100}{100+200} \\[10pt] &= 12 \times \frac{100}{300} \\[10pt] &= 4\text{ V} \end{aligned} \]
\[ \begin{aligned} V_{R2} &= 12 \times \frac{200}{100+200} \\[10pt] &= 12 \times \frac{200}{300} \\[10pt] &= 8\text{ V} \end{aligned} \]
分流の例: 100Ωと200Ωの抵抗が並列接続され、全体に0.3Aの電流が流れる場合
\[ \begin{aligned} I_{R1} &= 0.3 \times \frac{200}{100+200} \\[10pt] &= 0.3 \times \frac{200}{300} \\[10pt] &= 0.2\text{ A} \end{aligned} \]
\[ \begin{aligned} I_{R2} &= 0.3 \times \frac{100}{100+200} \\[10pt] &= 0.3 \times \frac{100}{300} \\[10pt] &= 0.1\text{ A} \end{aligned} \]
分流の法則で特に注意すべきは、分子に来る抵抗が「もう一方の抵抗」になることです。これは分圧の法則と異なる点です。
覚え方の一つとして:「電流は抵抗の少ない方に多く流れる」という物理的感覚で考えると理解しやすいでしょう。
応用例題
これまで学んだ重ね合わせの理、合成抵抗、分圧・分流の法則を使って、実際の回路問題を解いてみましょう。
例題1:重ね合わせの理の応用
以下の回路で抵抗 \(R_3\) に流れる電流を求めよ。
\(E_1 = 12\text{ V}, E_2 = 6\text{ V}, R_1 = 2\text{ kΩ}, R_2 = 4\text{ kΩ}, R_3 = 6\text{ kΩ}\)
解法:
- \(E_1\) のみを考慮し、\(E_2\) を短絡(0V)する:
- \[ \begin{aligned} R_{23} &= \frac{R_2 \times R_3}{R_2 + R_3} \\[10pt] &= \frac{4 \times 6}{4 + 6} \\[10pt] &= \frac{24}{10} \\[10pt] &= 2.4\text{ kΩ} \end{aligned} \]
- \[ \begin{aligned} I_1 &= \frac{E_1}{R_1 + R_{23}} \\[10pt] &= \frac{12}{2 + 2.4} \\[10pt] &= \frac{12}{4.4} \\[10pt] &\approx 2.73\text{ mA} \end{aligned} \]
- \[ \begin{aligned} I_{R3(1)} &= I_1 \times \frac{R_2}{R_2 + R_3} \\[10pt] &= 2.73 \times \frac{4}{4 + 6} \\[10pt] &= 2.73 \times \frac{4}{10} \\[10pt] &= 2.73 \times 0.4 \\[10pt] &\approx 1.09\text{ mA} \end{aligned} \]
- \(E_2\) のみを考慮し、\(E_1\) を短絡(0V)する:
- \[ \begin{aligned} R_{12} &= \frac{R_1 \times R_2}{R_1 + R_2} \\[10pt] &= \frac{2 \times 4}{2 + 4} \\[10pt] &= \frac{8}{6} \\[10pt] &\approx 1.33\text{ kΩ} \end{aligned} \]
- \[ \begin{aligned} I_2 &= \frac{E_2}{R_{12} + R_3} \\[10pt] &= \frac{6}{1.33 + 6} \\[10pt] &\approx \frac{6}{7.33} \\[10pt] &\approx 0.82\text{ mA} \end{aligned} \]
- \(R_3\) に流れる電流 \(I_{R3(2)} = I_2 = 0.82\text{ mA}\)
- 重ね合わせ:\(I_{R3} = I_{R3(1)} + I_{R3(2)} = 1.09 + 0.82 = 1.91\text{ mA}\)
例題2:分圧・分流回路の解析
以下の回路における抵抗 \(R_3\) にかかる電圧と抵抗 \(R_4\) に流れる電流を求めよ。
\(E = 24\text{ V}, R_1 = 2\text{ kΩ}, R_2 = 4\text{ kΩ}, R_3 = 3\text{ kΩ}, R_4 = 6\text{ kΩ}\)
解法:
- \(R_1\) と \(R_2\) の並列合成抵抗を求める:
\(R_{12} = \frac{R_1 R_2}{R_1 + R_2} = \frac{2 \times 4}{2 + 4} = \frac{8}{6} \approx 1.33\text{ kΩ}\)
- 分圧の法則を使って \(R_3\) にかかる電圧を求める:
\(V_{R3} = E \times \frac{R_3}{R_{12} + R_3} = 24 \times \frac{3}{1.33 + 3} \approx 24 \times \frac{3}{4.33} \approx 16.63\text{ V}\)
- \(R_3\) と \(R_4\) に同じ電圧がかかることから、\(R_4\) に流れる電流を求める:
\(I_{R4} = \frac{V_{R3}}{R_4} = \frac{16.63}{6} \approx 2.77\text{ mA}\)
- 回路を解析する際は、まず回路の構造を理解し、簡略化できる部分を見つけることが重要
- 合成抵抗の計算や分圧・分流の法則を適切に適用することで、計算が大幅に簡略化できる
- 複雑な回路でも、基本法則を組み合わせることで解析可能
🔍 ワンポイントアドバイス: 電気回路の解析では、「重ね合わせの理」「合成抵抗の計算」「分圧・分流の法則」を組み合わせることで、複雑な回路も効率的に解くことができます。特に分流の法則では、分子の抵抗が「もう一方の抵抗」になることを忘れないようにしましょう。また、回路解析の際は、まず回路を簡略化できないか考え、必要に応じて等価回路に置き換えることで計算を簡単にすることができます。電気回路の問題では、計算ミスを防ぐために単位(Ω、V、A)を常に意識し、有効数字にも注意することが大切です。
よっしゃ、今回はこの下図の回路を使って、電源 \( V_1 = 60\,\mathrm{V} \) だけを考えてみるで!
図1を見てみてな〜。この回路では、一番右側にある \( R_2 = 60\,\Omega \) が並列になってるやろ?
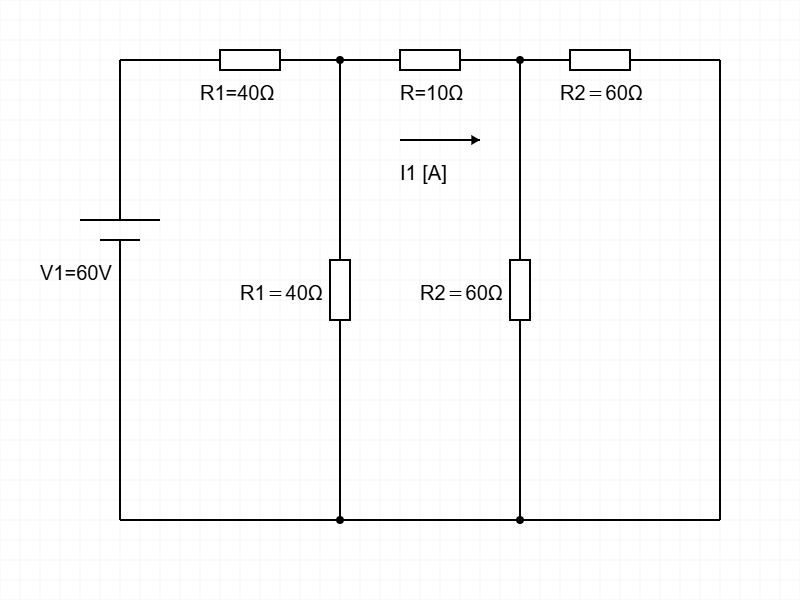
せやから、まずはこの2つの \( R_2 \) を合成して、並列抵抗を出してみよか。
ヒントや!並列合成抵抗の公式は、
\( R = \frac{R_1 \cdot R_2}{R_1 + R_2} \) やで!
はい、先生!
上下の \( R_2 = 60\,\Omega \) は並列なので、次のように合成します。
\[ R_2' = \frac{R_2 \cdot R_2}{R_2 + R_2} = \frac{60 \cdot 60}{60 + 60} \]
\[ R_2' = \frac{3600}{120} = 30\,\Omega \]
なるほど、\( R_2 \) の並列合成抵抗は \( 30\,\Omega \) になるんですね!
ええ感じやで〜!次は、この合成抵抗 \( R_2' = 30\,\Omega \) と、その右にある抵抗 \( R = 10\,\Omega \) の合成を考えるで!
この2つは直列やから、足し算すればええんやったな?
ほな、直列合成抵抗 \( R' \) を求めてみて!
はい、先生!
直列接続なので、抵抗をそのまま足し算します。
\[ R' = R + R_2' = 10 + 30 = 40\,\Omega \]
なるほど、直列の合成抵抗は \( 40\,\Omega \) になりますね!
よっしゃ次いこか〜!
いま求めた直列合成抵抗 \( R' = 40\,\Omega \) と、左側の抵抗 \( R_1 = 40\,\Omega \) を見てみて。
これらは回路図上で両端が同じノードに接続されてるから、並列接続になってるんや。
せやから、次はこの2つの並列合成抵抗 \( R_1' \) を計算してみてな!
ヒントや! 並列合成は掛け算割り算で、公式はこうやで:
\( R = \frac{R_1 \cdot R_2}{R_1 + R_2} \)
はい、先生!
\( R_1 = 40\,\Omega \)、\( R' = 40\,\Omega \) の並列接続なので、公式に当てはめると、
\[ R_1' = \frac{R_1 \cdot R'}{R_1 + R'} = \frac{40 \cdot 40}{40 + 40} \]
\[ R_1' = \frac{1600}{80} = 20\,\Omega \]
並列合成抵抗は \( 20\,\Omega \) になります!
よっしゃ次いこか〜!
いま求めた直列合成抵抗 \( R' = 40\,\Omega \) と、左側の抵抗 \( R_1 = 40\,\Omega \) を見てみて。
これらは回路図上で両端が同じノードに接続されてるから、並列接続になってるんや。
せやから、次はこの2つの並列合成抵抗 \( R_1' \) を計算してみてな!
ヒントや! 並列合成は掛け算割り算で、公式はこうやで:
\( R = \frac{R_1 \cdot R_2}{R_1 + R_2} \)
はい、先生!
\( R_1 = 40\,\Omega \)、\( R' = 40\,\Omega \) の並列接続なので、公式に当てはめると、
\[ R_1' = \frac{R_1 \cdot R'}{R_1 + R'} = \frac{40 \cdot 40}{40 + 40} \]
\[ R_1' = \frac{1600}{80} = 20\,\Omega \]
並列合成抵抗は \( 20\,\Omega \) になります!
よっしゃここまで来たら、電源 \( V_1 = 60\,\mathrm{V} \) を使って、電流を求めていくで!
いま合成した並列抵抗 \( R_1' = 20\,\Omega \) の右に、もうひとつ \( R_1 = 40\,\Omega \) が直列につながってるな?
ということは、回路全体の合成抵抗は \( R_1' + R_1 \) になるんや。
この合成抵抗に対して電圧が \( 60\,\mathrm{V} \) かかるから、電流 \( I_{\mathrm{v1}} \) を求めてみよか!
はい、先生!
合成抵抗は次の通りです:
\[ R_{\text{total}} = R_1' + R_1 = 20 + 40 = 60\,\Omega \]
オームの法則 \( I = \frac{V}{R} \) に当てはめて、
\[ I_{\mathrm{v1}} = \frac{V_1}{R_{\text{total}}} = \frac{60}{60} = 1\,\mathrm{A} \]
ということで、電源 \( V_1 \) を流れる電流は \( 1\,\mathrm{A} \) になります!
よっしゃ次いこか〜!
いま求めた直列合成抵抗 \( R' = 40\,\Omega \) と、左側の抵抗 \( R_1 = 40\,\Omega \) を見てみて。
これらは回路図上で両端が同じノードに接続されてるから、並列接続になってるんや。
せやから、次はこの2つの並列合成抵抗 \( R_1' \) を計算してみてな!
ヒントや! 並列合成は掛け算割り算で、公式はこうやで:
\( R = \frac{R_1 \cdot R_2}{R_1 + R_2} \)
はい、先生!
\( R_1 = 40\,\Omega \)、\( R' = 40\,\Omega \) の並列接続なので、公式に当てはめると、
\[ R_1' = \frac{R_1 \cdot R'}{R_1 + R'} = \frac{40 \cdot 40}{40 + 40} \]
\[ R_1' = \frac{1600}{80} = 20\,\Omega \]
並列合成抵抗は \( 20\,\Omega \) になります!
よっしゃここまで来たら、電源 \( V_1 = 60\,\mathrm{V} \) を使って、電流を求めていくで!
いま合成した並列抵抗 \( R_1' = 20\,\Omega \) の右に、もうひとつ \( R_1 = 40\,\Omega \) が直列につながってるな?
ということは、回路全体の合成抵抗は \( R_1' + R_1 \) になるんや。
この合成抵抗に対して電圧が \( 60\,\mathrm{V} \) かかるから、電流 \( I_{\mathrm{v1}} \) を求めてみよか!
はい、先生!
合成抵抗は次の通りです:
\[ R_{\text{total}} = R_1' + R_1 = 20 + 40 = 60\,\Omega \]
オームの法則 \( I = \frac{V}{R} \) に当てはめて、
\[ I_{\mathrm{v1}} = \frac{V_1}{R_{\text{total}}} = \frac{60}{60} = 1\,\mathrm{A} \]
ということで、電源 \( V_1 \) を流れる電流は \( 1\,\mathrm{A} \) になります!
ほな最後の仕上げや!
今求めた電流 \( I_{\mathrm{v1}} = 1\,\mathrm{A} \) は、直列抵抗 \( R_1 = 40\,\Omega \) と \( R' = 40\,\Omega \) に分かれて流れるんや。
このとき、抵抗 \( R = 10\,\Omega \) を通る電流(つまり分流した電流)\( I_1 \) を求めるには、**分流の法則**を使えばええねん!
ヒントやで!
\( I_1 = \frac{R_1}{R' + R_1} \times I_{\mathrm{v1}} \)
この式に数値を代入して、\( I_1 \) を求めてみて!
はい、先生!
分流の法則を使って、\( I_1 \) を求めてみます。
\[ I_1 = \frac{R_1}{R' + R_1} \times I_{\mathrm{v1}} = \frac{40}{40 + 40} \times 1 \]
\[ I_1 = \frac{40}{80} = 0.5\,\mathrm{A} \]
ということで、抵抗 \( R \) を流れる電流 \( I_1 \) は \( 0.5\,\mathrm{A} \) になります!
さて次はステップ2やで!
今度は電源 \( V_2 = 80\,\mathrm{V} \) だけを考えた回路を見てみよか。
図はこんな感じになってるで:
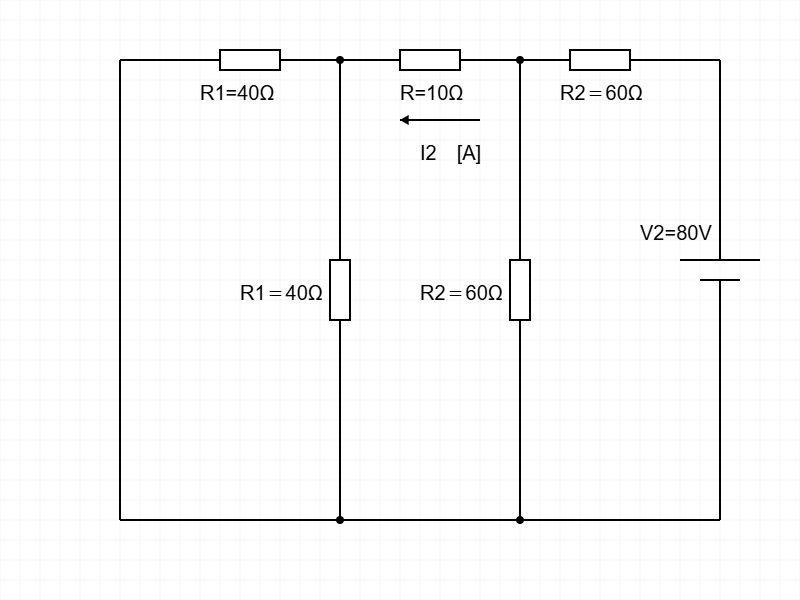
ここで、一番左側にある \( R_1 = 40\,\Omega \) が並列になってるやろ?
せやから、まずはこの2つの \( R_1 \) を合成して、並列抵抗を出してみてや!
ヒントやで〜!
\( R = \frac{R_1 \cdot R_1}{R_1 + R_1} \) や!
はい、先生!
上下の \( R_1 = 40\,\Omega \) は並列接続なので、合成抵抗は:
\[ R_1'' = \frac{R_1 \cdot R_1}{R_1 + R_1} = \frac{40 \cdot 40}{40 + 40} \]
\[ R_1'' = \frac{1600}{80} = 20\,\Omega \]
ということで、並列合成抵抗 \( R_1'' \) は \( 20\,\Omega \) になります!
ええ感じやな!次は、今求めた \( R_1'' = 20\,\Omega \) と中央の抵抗 \( R = 10\,\Omega \) を見てみて。
この2つは一直線につながってるから、直列接続やな。
ということは、単純に足し算すれば合成抵抗 \( R'' \) が求まるで!
さっそく計算してみよか〜!
はい、先生!
直列接続なので、合成抵抗はそのまま足し算ですね。
\[ R'' = R + R_1'' = 10 + 20 = 30\,\Omega \]
ということで、\( R'' \) は \( 30\,\Omega \) になります!
ええ感じやな!次は、今求めた \( R_1'' = 20\,\Omega \) と中央の抵抗 \( R = 10\,\Omega \) を見てみて。
この2つは一直線につながってるから、直列接続やな。
ということは、単純に足し算すれば合成抵抗 \( R'' \) が求まるで!
さっそく計算してみよか〜!
はい、先生!
直列接続なので、合成抵抗はそのまま足し算ですね。
\[ R'' = R + R_1'' = 10 + 20 = 30\,\Omega \]
ということで、\( R'' \) は \( 30\,\Omega \) になります!
ええ調子やで!
今求めた直列合成抵抗 \( R'' = 30\,\Omega \) と、右側の抵抗 \( R_2 = 60\,\Omega \) を見てみて。
この2つは両端が同じノードにつながってるから、並列接続やな!
せやから、合成抵抗 \( R_2'' \) を求めるには並列の公式を使えばええ。
ヒントやで〜!
\( R = \frac{R_1 \cdot R_2}{R_1 + R_2} \)
はい、先生!
\( R'' = 30\,\Omega \)、\( R_2 = 60\,\Omega \) を並列合成するので、
\[ R_2'' = \frac{R'' \cdot R_2}{R'' + R_2} = \frac{30 \cdot 60}{30 + 60} \]
\[ R_2'' = \frac{1800}{90} = 20\,\Omega \]
ということで、合成抵抗 \( R_2'' \) は \( 20\,\Omega \) になります!
ほな次いくで〜!
今求めた合成抵抗 \( R_2'' = 20\,\Omega \) の右に、さらにもうひとつの \( R_2 = 60\,\Omega \) が直列でつながってるんや。
ということは、回路全体にかかる合成抵抗は \( R_2'' + R_2 \) やな!
この合成抵抗に対して、電圧 \( V_2 = 80\,\mathrm{V} \) がかかるから、電流 \( I_{\mathrm{v2}} \) を求めてみよか!
ヒントや!
オームの法則やで〜: \( I = \frac{V}{R} \)
はい、先生!
合成抵抗は:
\[ R_{\text{total}} = R_2'' + R_2 = 20 + 60 = 80\,\Omega \]
電圧は \( V_2 = 80\,\mathrm{V} \) なので、
\[ I_{\mathrm{v2}} = \frac{V_2}{R_{\text{total}}} = \frac{80}{80} = 1\,\mathrm{A} \]
ということで、電源 \( V_2 \) を流れる電流は \( 1\,\mathrm{A} \) です!
よっしゃ仕上げにいくで〜!
電源 \( V_2 = 80\,\mathrm{V} \) からの電流 \( I_{\mathrm{v2}} = 1\,\mathrm{A} \) が、\( R'' = 30\,\Omega \) と \( R_2 = 60\,\Omega \) に分かれて流れてるんやったな?
せやから、分流の法則を使って抵抗 \( R \) を流れる電流 \( I_2 \) を求めてみよか!
ヒントや!
分流の公式はこんな感じやで:
\( I_2 = \frac{R_2}{R'' + R_2} \times I_{\mathrm{v2}} \)
はい、先生!
では、分流の公式に代入して計算してみます。
\[ I_2 = \frac{60}{30 + 60} \times 1 = \frac{60}{90} = 0.6667\,\mathrm{A} \]
ということで、抵抗 \( R \) を流れる電流 \( I_2 \) は約 \( 0.6667\,\mathrm{A} \) です!
よっしゃ仕上げにいくで〜!
電源 \( V_2 = 80\,\mathrm{V} \) からの電流 \( I_{\mathrm{v2}} = 1\,\mathrm{A} \) が、\( R'' = 30\,\Omega \) と \( R_2 = 60\,\Omega \) に分かれて流れてるんやったな?
せやから、分流の法則を使って抵抗 \( R \) を流れる電流 \( I_2 \) を求めてみよか!
ヒントや!
分流の公式はこんな感じやで:
\( I_2 = \frac{R_2}{R'' + R_2} \times I_{\mathrm{v2}} \)
はい、先生!
では、分流の公式に代入して計算してみます。
\[ I_2 = \frac{60}{30 + 60} \times 1 = \frac{60}{90} = 0.6667\,\mathrm{A} \]
ということで、抵抗 \( R \) を流れる電流 \( I_2 \) は約 \( 0.6667\,\mathrm{A} \) です!
さあ最終ステップや!
今までに、抵抗 \( R \) に流れる電流を 2つ求めたやろ?
- \( I_1 = 0.5\,\mathrm{A} \):\( V_1 = 60\,\mathrm{V} \) のとき
- \( I_2 = 0.6667\,\mathrm{A} \):\( V_2 = 80\,\mathrm{V} \) のとき
この2つの電流、流れる方向に注意して重ね合わせせなあかんで!
今回は \( I_2 \) の方が \( R \) に流れ込む、\( I_1 \) は流れ出す方向とすると、
重ね合わせの結果としての電流 \( I \) は:
\( I = I_2 - I_1 \)
これを使って、最終的な電流 \( I \) と、\( R = 10\,\Omega \) によって消費される電力 \( P \) を求めてみて!
ヒント: \( P = RI^2 \) やで!
はい、先生!
まず電流 \( I \) を求めます。
\[ \begin{aligned} I &= I_2 - I_1 \\[10pt] &= 0.6667 - 0.5 \\[10pt] &= 0.1667\,\mathrm{A} \end{aligned} \]
次に電力 \( P \) を求めます。
\[ \begin{aligned} P &= RI^2 \\[10pt] &= 10 \times (0.1667)^2 \\[10pt] &= 10 \times 0.02779 \\[10pt] &= 0.2779\,\mathrm{W} \end{aligned} \]
よって、消費電力は約 \( 0.28\,\mathrm{W} \) になります!
解説まとめ
電源\( V_1 = 60 \ \mathrm{[V]} \)と\( V_2 = 80 \ \mathrm{[V]} \)を個別に考え、重ね合わせの理を使って電流を合算する。
抵抗R_2の並列合成抵抗\( R_2' \)は以下の通り:
\[ \begin{eqnarray} R_2' &=& \frac{R_2 \cdot R_2}{R_2 + R_2} \\[15pt] &=& \frac{R_2}{2} \\[15pt] &=& \frac{60}{2} \\[15pt] &=& 30 \ \mathrm{[\Omega]} \end{eqnarray} \]
この\( R_2' \)とRの直列合成抵抗\( R' \)は:
\[ \begin{eqnarray} R' &=& R + R_2' \\[15pt] &=& 10 + 30 \\[15pt] &=& 40 \ \mathrm{[\Omega]} \end{eqnarray} \]
さらに、\( R' \)とR_1の並列合成抵抗\( R_1' \)は:
\[ \begin{eqnarray} R_1' &=& \frac{R' \cdot R_1}{R' + R_1} \\[15pt] &=& \frac{40 \times 40}{40 + 40} \\[15pt] &=& 20 \ \mathrm{[\Omega]} \end{eqnarray} \]
よって、電源V_1による電流\( I_{\mathrm{v1}} \)は:
\[ \begin{eqnarray} I_{\mathrm{v1}} &=& \frac{V_1}{R_1' + R_1} \\[15pt] &=& \frac{60}{20 + 40} \\[15pt] &=& 1 \ \mathrm{[A]} \end{eqnarray} \]
抵抗Rを流れる電流\( I_1 \)は分流の法則より:
\[ \begin{eqnarray} I_1 &=& \frac{R_1}{R' + R_1} \times I_{\mathrm{v1}} \\[15pt] &=& \frac{40}{40 + 40} \times 1 \\[15pt] &=& 0.5 \ \mathrm{[A]} \end{eqnarray} \]
次に、R_1の並列合成抵抗\( R_1'' \)は:
\[ \begin{eqnarray} R_1'' &=& \frac{R_1 \cdot R_1}{R_1 + R_1} \\[15pt] &=& \frac{R_1}{2} \\[15pt] &=& \frac{40}{2} \\[15pt] &=& 20 \ \mathrm{[\Omega]} \end{eqnarray} \]
この\( R_1'' \)とRの直列合成抵抗\( R'' \)は:
\[ \begin{eqnarray} R'' &=& R + R_1'' \\[15pt] &=& 10 + 20 \\[15pt] &=& 30 \ \mathrm{[\Omega]} \end{eqnarray} \]
これとR_2の並列合成抵抗\( R_2'' \)は:
\[ \begin{eqnarray} R_2'' &=& \frac{R'' \cdot R_2}{R'' + R_2} \\[15pt] &=& \frac{30 \times 60}{30 + 60} \\[15pt] &=& 20 \ \mathrm{[\Omega]} \end{eqnarray} \]
電源V_2による電流\( I_{\mathrm{v2}} \)は:
\[ \begin{eqnarray} I_{\mathrm{v2}} &=& \frac{V_2}{R_2'' + R_2} \\[15pt] &=& \frac{80}{20 + 60} \\[15pt] &=& 1 \ \mathrm{[A]} \end{eqnarray} \]
よって、Rを流れる電流\( I_2 \)は:
\[ \begin{eqnarray} I_2 &=& \frac{R_2}{R'' + R_2} \times I_{\mathrm{v2}} \\[15pt] &=& \frac{60}{30 + 60} \times 1 \\[15pt] &\approx& 0.6667 \ \mathrm{[A]} \end{eqnarray} \]
電流の向きを考慮すると、抵抗Rを流れる合成電流\( I \)は:
\[ \begin{eqnarray} I &=& I_2 - I_1 \\[15pt] &=& 0.6667 - 0.5 \\[15pt] &\approx& 0.1667 \ \mathrm{[A]} \end{eqnarray} \]
したがって、抵抗で消費される電力\( P \)は:
\[ \begin{eqnarray} P &=& R \cdot I^2 \\[15pt] &=& 10 \times 0.1667^2 \\[15pt] &\approx& 0.2779 \rightarrow 0.28 \ \mathrm{[W]} \end{eqnarray} \]